Introducere[]
Pendulul gravitaţional a fost studiat pentru prima dată în profunzime de către savantul italian Galileo Galilei şi aplicat în studierea mişcării corpurilor.
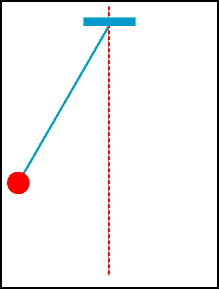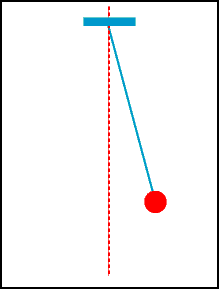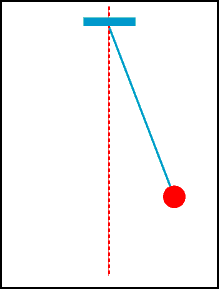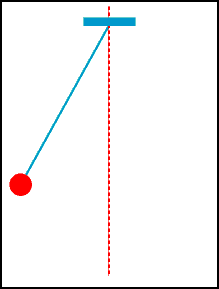
Este format dintr-un corp de masă m şi de dimensiuni mici (punct material) suspendat de un fir inextensibil, cu masă neglijabilă, de lungime l. Dacă pendulul este scos din poziţia sa de echilibru şi este lăsat liber, el efectuează o mişcare oscilatorie într-un plan vertical, datorită forţei de greutate. In fig. 1 este reprezentat un astfel de pendul, care formează cu verticala un unghi numit elongaţie unghiulară.
Componenta greutăţii în lungul firului (normală la traiectoria arc de cerc a pendulului), este compensată de tensiunea din fir, T. Componenta tangenţială la traiectorie, este forţa de revenire (de rapel) care acţionează asupra pendulului spre a-l readuce în poziţia de echilibru.
Se observă că forţa de revenire nu este proporţională cu elongaţia unghiulară, deci oscilaţiile pendulului nu sunt armonice, în general. Insă pentru unghiuri suficient de mici, exprimat în radiani(de exemplu, pentru ), astfel că forţa de revenire devine proporţională cu elongaţia unghiulară, iar oscilaţiile pot fi considerate armonice.
Din fig.1 se vede că elongaţia unghiulară θ = x/l , unde x este lungimea arcului de cerc corespunzător, astfel că forţa de revenire se poate scrie:
- (1)
în care mărimea:
- (2)
reprezintă constanta elastică a sistemului. Din (1) se observă că forţa de revenire a sistemului este proporţională cu elongaţia x, iar din figură se vede că este mereu de sens opus elongaţiei (când elongaţia este spre dreapta, forţa de revenire este orientată spre stânga, şi invers). O asemenea forţă de revenire este denumită de tip elastic, iar sistemul fizic supus unei astfel de forţe efectuează oscilaţii armonice cu perioada dată de:
- (3)
Ţinând seamă de (2) şi (3), rezultă că perioada de oscilaţie a pendulului gravitaţional este dată de:
- (4)
Izocronicitatea micilor oscilaţii[]
Perioada unei oscilaţii efectuate de un pendul gravitaţional rămâne constantă, indiferent de masa corpului atârnat de fir, atunci când oscilaţiile sunt mici.
Oscilaţiile cu o amplitudine mai mare, unde deviaţia firului faţă de poziţia de echilibru depăşeşte nu sunt izocrone. Pentru ca oscilaţiile să aibă aceeaşi perioadă indiferent de amplitudine, traiectoria circulară trebuie înlocuită cu o traiectorie cicloidală, după cum a demonstrat Christiaan Huygens, care a folosit acest principiu când a construit pendulul cicloidal.
Mărimi fizice caracteristice[]
În cazul oscilaţiilor de amplitudine mică, perioada unei oscilaţii complete efectuate de pendululu galilean este dată de formula:
unde
perioada (măsurată în secunde)
(raportul dintre lungimea circumferinţei unui cerc şi diametru lui)
lungimea firului (exprimată în metri)
acceleraţia gravitaţională, aproximativ (depinde de locul de pe glob unde se efectuează măsurarea şi de altitudine)
La amplitudini mai mari, perioada se poate calcula folosind o serie infinită:
unde este amplitudinea unghiulară a pendulului.
Dispozitive experimentale bazate pe pendulul gravitaţional[]
- Pendulul balistic
- Pendulul dublu
- Pendulul Huygens (pendul cicloidal)
- Pendulul Foucault
- Pendulul Kater (pendul reversibil)
- Pendulul Overbeck
Determinarea experimentală a acceleraţiei gravitaţionale[]
Din (4) rezultă că perioada oscilaţiilor mici ale pendulului gravitaţional este independentă de masa pendulului şi de amplitudinea oscilaţiilor, ea depinde numai de lungimea pendulului (g fiind constant pentru locul dat al experimentului).
Să verificăm legea de dependenţă a perioadei pendulului gravitaţional de lungimea lui, iar în partea a doua să determinăm acceleraţia gravitaţională din locul experienţei, observând din (4) că, dacă se măsoară cu o eroare cât mai mică lungimea l şi perioada proprie T , se poate calcula acceleraţia gravitaţională g.
Mod de lucru[]
1. Folosind materialele din laborator, se realizează un pendul gravitaţional cu lungimea l=0,2m;
2. Se scoate pendulul din poziţia de echilibru şi, după ce este lăsat liber, se măsoară timpul t în care se efectuează n=20 de oscilaţii de amplitudine mică;
3. Se calculează perioada oscilaţiilor T=t/n;
4. Se măreşte succesiv lungimea pendulului cu câte 0,1 m, măsurând perioada pendulelor astfel formate, ca la pct.2 şi 3;
5. Cu datele măsurate se completează tabelul de mai jos şi apoi se reprezintă grafic
6. Se interpretează rezultatul obţinut.
7. Folosind relaţia (4) pentru fiecare din pendulele formate, se calculează acceleraţia gravitaţională g, precum şi valoarea sa medie; datele se trec în tabel.
| Nr. crt. | l(m) | n | t(s) | T(s) | |||
|---|---|---|---|---|---|---|---|
| 1 | 0,2 | ||||||
| 2 | 0,3 | ||||||
| 3 | 0,4 | ||||||
| 4 | 0,5 | ||||||
| 5 | 0,6 | ||||||
| 6 | 0,7 |