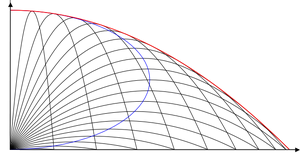
Traiectoriile parabolice ale unui proiectil lansat cu aceeaşi viteză dar în unghiuri diferite. Cu roşu este trasată parabola de siguranţă.
În fizică şi mai ales în balistică, termenul parabolă de siguranță reprezintă înfășurătoarea tuturor traiectoriilor parabolice ale unui proiectil lansat dintr-un punct dat, cu o anumită viteză şi într-un anumit plan vertical. Denumirea provine de la faptul că niciun punct aflat în exteriorul acestei curbe nu poate fi atins de proiectilul care respectă condiţiile indicate (referitoare la viteză şi la punctul de lansare).
În coordonate carteziene, această parabolă este descrisă de ecuaţia:
unde:
- modulul vitezei iniţiale de lansare,
- g= accelerația gravitațională terestră,
- este înălţimea maximă ce poate fi atinsă de proiectil.
Ecuaţia parabolei de siguranţă[]
Fie proiectilul P lansat în vid din punctul O cu viteza iniţială Traiectoria sa este o parabolă situată în planul vertical :
Ecuaţia carteziană a acestei parabole este:
unde este unghiul sub care este lansat proiectilul, adică cel format de cu orizontala.
Pentru a ajunge în punctul unghiul trebuie să satisfacă relaţia:
Aceasta este o ecuaţie de gradul al doilea cu necunoscuta care are două soluţii, una dublă sau niciuna după cum discriminantul este pozitiv, nul sau negativ. În cazul limită, punctul M se situează pe curba de siguranţă (C). Avem:
de unde obţinem ecuaţia parabolei de siguranţă:
Avem pentru care este distanţa maximă orizontală.
Vezi şi[]
- Elipsă de siguranță
















