[]
Noţiunea de lucru mecanic a apărut din necesitatea de a măsura munca (fizică) depusă de om, precum şi de maşinile construite de el pentru a-i ajuta în această muncă.
Să considerăm situaţia simplă în care un buştean este deplasat pe un plan orizontal cu ajutorul unui cablu de către un om. Aceeaşi deplasare se poate realiza şi cu ajutorul unui cal sau al unui tractor. Generalizând până la abstractizare interacţiunea care se realizează prin intermediul cablului între buştean pe de o parte şi om, cal sau tractor pe de altă parte, s-a ajuns la noţiunea de forţă. Această noţiune ne permite să facem abstracţie de situaţia concretă considerată şi în loc să spunem că omul munceşte, vom spune că forţa F produce un lucru mecanic. Lucrul mecanic al forţei F este cu atât mai mare cu cât intensitatea forţei şi deplasarea corpului (asupra căruia acţionează forţa) sunt mai mari. Pentru generalizare, se poate face abstracţie şi de corpul considerat şi spune că o forţă produce lucru mecanic atunci când punctul său de aplicaţie se deplasează. O forţă care acţionează asupra unui rigid are caracterul unui vector alunecător, adică efectul forţei nu se schimbă dacă punctul de aplicaţie se deplasează pe suportul ei. Trebuie observat că în cadrul noţiunii de lucru mecanic al unei forţe nu o astfel de deplasare este luată în considerare, ci deplasarea efectivă a punctului de pe corp în care se consideră aplicată forţa.
Denumirea de lucru (travail d'une force) a fost dată de inginerul francez Gaspard-Gustave Coriolis. Conţinutul noţiunii s-a adâncit, o dată cu cea de căldură, în secolul al XlX-lea când s-a dovedit experimental că există un raport constant între valoarea numerica a lucrului mecanic (care este legat de mişcarea mecanică) şi cantitatea de căldură (care este legată de o formă de mişcare nemecanică a materiei) în care acesta se poate transforma.
Proprietăţi ale lucrului mecanic[]
a) este o mărime scalară având ca unitate de măsură în sistemul internaţional SI joule-ul (J) şi în sistemul tehnic kilogram - forţă - metrul (kgf.m);
b) este pozitiv când şi poartă în acest caz numele de lucru mecanic motor
c) este negativ când şi poartă în acest caz numele de lucru mecanic rezistent
d) este nul când
e) dacă deplasarea este compusă din n deplasări elementare:
- (5)
atunci:
- (6)
Deci: lucrul mecanic elementar corespunzător unei deplasări compuse este egal cu suma lucrurilor mecanice elementare aferente deplasărilor componente;
f) dacă forţa F reprezintă rezultanta unică a unui sistem de forţe:
- (7)
atunci lucrul mecanic este:
- (8)
Adică, lucrul mecanic elementar corespunzător rezultantei unui sistem de forţe este egal cu suma algebrică a lucrurilor mecanice elementare ale forţelor componente.
Lucrul mecanic total[]

Fig. 2
Când este corespunzător unei forţe variabile şi unei deplasări finite a punctului material între punctele A şi B pe o traiectorie curbilinie (figura 2) lucrul mecanic este dat de expresia:
- (9)
iar în cazul unui cuplu:
- (10)
Expresia (9) se obţine prin descompunerea mişcării finite în mişcării elementare pentru care forţa se consideră constantă., iar arcul de curbă se aproximează cu coarda şi însumarea lucrurilor mecanice elementare corespunzătoare. Din relaţia (9) se observă că lucrul mecanic corespunzător unei deplasări finite a unui punct material şi unei forţe variabile depind atât de modul cum variază forţa, cât şi de forma traiectoriei.
Lucrul mecanic în cazul forţelor conservative[]
În cazul în care forţa F este conservativă expresia ei este:
- (11)
unde este funcţia de forţă.
Funcţia de forţă este o funcţie scalară de coordonatele punctului, cu ajutorul căreia se pot determina componentele forţei astfel:
Pentru a exista o funcţie de forţă trebuie îndeplinite condiţiile lui Cauchy, care sunt :
Lucrul mecanic elementar este:
- (12)
- (13)
Lucrul mecanic total este:
- (14)
unde şi sunt funcţiile de forţă corespunzătoare poziţiilor iniţială şi finală.
Rezultă că: lucrul mecanic total în cazul unei forţe conservative depinde numai de poziţiile
iniţială şi finală ale punctului, fiind independent de forma traiectoriei.
În locul funcţiei U, se poate considera funcţia V, numită şi funcţie potenţial şi definită prin
relaţia: Nu s-a putut interpreta (eroare de sintaxă): {\displaystyle V = −U \!.}
În acest caz, lucrul mecanic elementar are expresia Nu s-a putut interpreta (eroare de sintaxă): {\displaystyle dL = −dV \!.}
Funcţia de forţă U şi funcţia potenţial V nu pot fi determinate decât cu aproximaţia unei constante.
Dacă un punct material este acţionat simultan de un sistem de forţe conservative care derivă din funcţiile de forţă astfel încât:
Rezultanta va avea proiecţiile:
adică rezultanta derivă din funcţia de forţă Un astfel de sistem de forţe se numeşte sistem conservativ.
Exemple[]

Fig. 3
a) Forţa este constantă ca modul şi direcţie iar traiectoria este o curbă oarecare (fig. 3). Faţă de mamamamama
- (15)
deci:
- (16)
Rezultă (17)
unde este unghiul dintre segmentul de dB şi axa Ox.
Semnul plus se iareaptă A când punctul coboară, iar semnul minus când punctul urcă.
b) În cazul în care este o forţă gravitaţională (figura 4) notând-o cu G, rezultă:

Fig. 4
- (18)
În general:
- (19)
Rezultă că: lucrul mecanic al unei greutăţi nu depinde de forma traiectoriei pe care se deplasează punctul său de aplicaţie, ci depinde. numai de poziţiile extreme între care se efectuează mişcarea, fiind egal cu produsul dintre valoarea numerică a forţei şi diferenţa de cotă dintre poziţiile iniţială şi finală.
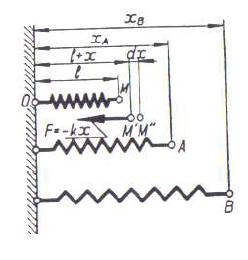
Fig. 5
c) Lucrul mecanic al unei forţe elastice. Se consideră un resort spiral OM în stare liberă fixat în punctul 0 (figura 5). Prin întinderea arcului cu lungimea x ia naştere o forţă proporţională cu alungirea resortului. Coeficientul de proporţionalitate notat prin k poartă numele de constantă elastică a resortului şi reprezintă forţa necesară pentru a produce o alungire a resortului egală cu unitatea. Pentru o deplasare elementară dx a punctului din în lucrul mecanic elementar corespunzător forţei elastice şi deplasării este :
- (20)
Pentru o deplasare finită din A în B a extremităţii M a resortului când acesta este întins, lucrul mecanic va fi:
- (21)
Lucrul mecanic elementar corespunzător unui sistem de forţe ce acţionează asupra unui solid rigid[]
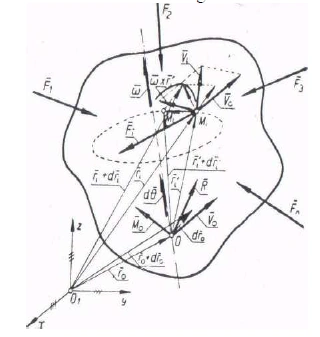
Fig. 6
Se consideră un solid rigid liber (figura 6), supus acţiunii unui sistem de forţe active
Lucrul mecanic elementar corespunzător forţei şi deplasării elementare a punctului de aplicaţie al forţei este:
- (22)
Notând cu:
- — viteza punctului O, aparţinând solidului rigid;
- — viteza unghiulară de rotaţie a solidului rigid faţă de punctul 0, relaţia (22) devine:
unde este vectorul de poziţie al punctului M faţă de punctul 0. Pentru întregul sistem de forţe se obţine:
Dar:
1. — deplasarea elementară prin translaţie a rigidului
2. — unghiul elementar de rotaţie considerat ca vector;
3. — vectorul rezultant al sistemului de forţe active;
4. — vectorul moment rezultant al sistemului de forţe active relativ la polul 0;
Adică:
- (23)
Un caz important în aplicaţiile tehnice este acela al
unui rigid acţionat de un cuplu Nu s-a putut interpreta (eroare de sintaxă): {\displaystyle (\vec F; −\vec F). \!}
În acest caz mişcarea rigidului este o rotaţie.
Având în vedere că din relaţia (23) se obţine:
- (24)
Când axa de rotaţie coincide cu suportul lui şi acesta este constant, rezultă:
- (25)
Lucrul mecanic al forţelor interioare[]

Fig. 7
Se consideră două puncte materiale şi asupra cărora acţionează forţele interioare şi respectiv (figura 7). Fie şi vectorii de poziţie ai punctelor şi în raport cu punctul fix 0.
Lucrul mecanic elementar aferent forţelor şi respectiv şi deplasărilor elementare ale punctelor de aplicaţie le forţelor este:
Deoarece rezultă că (26)
În expresia (26) este un scalar pozitiv sau negativ după cum punctele şi se resping sau se atrag.
Dacă punctele materiale aparţin unui sistem material rigid iar rezultă
că: suma lucrurilor mecanice elementare ale forţelor interioare ce acţionează punctele unui sistem
material rigid, pentru orice deplasare elementară a sistemului este nulă.
Reprezentarea grafică a lucrului mecanic[]
În figura 8 este arătată reprezentarea grafică a lucrului mecanic cu ajutorul unei diagrame.
În abscisă se reprezintă proiecţia deplasării pe direcţia forţei, iar în ordonată este reprezentată forţa. Lucrul mecanic corespunzător forţei şi deplasării finite este egal cu valoarea ariei dată de diagrama a:
- suprafaţa (27)
iar în cazul unui moment prin valoarea suprafeţei date de diagrama b.
Vezi şi[]
- Putere
- Legi de conservare
























































































