Fie o curbă spaţială dată prin ecuaţia ei vectorială:
Γ
:
r
→
=
r
→
(
t
)
,
M
0
(
t
0
)
{\displaystyle \Gamma :\;{\vec {r}}={\vec {r}}(t),\;\;M_{0}(t_{0})\!}
T
M
0
(
Γ
)
{\displaystyle T_{M_0} (\Gamma) \!}
M
0
.
{\displaystyle M_0. \!}
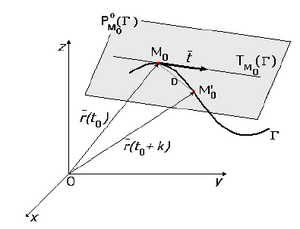
Definiţie .
Un plan care conţine dreapta tangentă c se numeşte plan tangent şi se notează
π
M
0
(
Γ
)
.
{\displaystyle \pi _{M_{0}}(\Gamma ).\!}
M
′
(
t
0
+
k
)
{\displaystyle M'(t_{0}+k)\!}
Γ
,
{\displaystyle \Gamma, \!}
M
0
,
{\displaystyle M_0, \!}
k fiind o creştere mică astfel ca
t
0
+
k
∈
I
.
{\displaystyle t_{0}+k\in I.\!}
D
(
M
0
,
M
0
′
)
{\displaystyle D(M_{0},M'_{0})\!}
Γ
.
{\displaystyle \Gamma. \!}
Observaţie .
Dreapta obţinută ca limită a poziţiilor secantelor
D
(
M
0
,
M
0
′
)
{\displaystyle D(M_{0},M'_{0})\!}
M
0
→
M
0
′
{\displaystyle M_{0}\to M'_{0}\!}
k
→
0
{\displaystyle k\to 0\!}
Γ
{\displaystyle \Gamma \!}
M
0
.
{\displaystyle M_0. \!}
Definiţie .
Planul determinat de dreapta
T
M
0
(
Γ
)
{\displaystyle T_{M_0} (\Gamma) \!}
M
0
′
{\displaystyle M'_{0}\!}
Γ
{\displaystyle \Gamma \!}
M
0
,
{\displaystyle M_0, \!}
plan osculator al curbei
Γ
{\displaystyle \Gamma \!}
M
0
,
{\displaystyle M_0, \!}
P
M
0
o
(
Γ
)
.
{\displaystyle P_{M_{0}}^{o}(\Gamma ).\!}
M
0
,
{\displaystyle M_0, \!}
r
→
˙
(
t
0
)
{\displaystyle {\dot {\vec {r}}}(t_{0})\!}
M
0
M
0
′
→
=
r
→
(
t
0
+
k
)
−
r
→
(
t
0
)
.
{\displaystyle {\overrightarrow {M_{0}M'_{0}}}={\vec {r}}(t_{0}+k)-{\vec {r}}(t_{0}).\!}
1
k
[
r
→
(
t
0
+
k
)
−
r
→
(
t
0
)
]
{\displaystyle {\frac {1}{k}}[{\vec {r}}(t_{0}+k)-{\vec {r}}(t_{0})]\!}
M
0
M
0
′
→
.
{\displaystyle {\overrightarrow {M_{0}M'_{0}}}.\!}
Planul osculator la o curbă spaţială
Fie
t
k
{\displaystyle t_{k}\!}
(
t
0
,
t
0
+
k
)
.
{\displaystyle (t_{0},t_{0}+k).\!}
r
→
(
t
)
{\displaystyle \vec r(t) \!}
C
2
{\displaystyle \mathcal C^2 \!}
I , putem considera aproximarea de ordinul II a expresiei
r
→
(
t
0
+
k
)
:
{\displaystyle {\vec {r}}(t_{0}+k):\!}
r
→
(
t
0
+
k
)
=
r
→
(
t
0
)
+
k
⋅
r
→
˙
(
t
0
)
+
k
2
2
!
⋅
r
→
¨
(
t
k
)
t
k
∈
(
t
0
,
t
0
+
k
)
{\displaystyle {\vec {r}}(t_{0}+k)={\vec {r}}(t_{0})+k\cdot {\dot {\vec {r}}}(t_{0})+{\frac {k^{2}}{2!}}\cdot {\ddot {\vec {r}}}(t_{k})\;\;t_{k}\in (t_{0},t_{0}+k)\!}
care se obţine din formula Taylor cu restul Lagrange aplicată funcţiei vectoriale
r
→
.
{\displaystyle {\vec {r}}.\!}
În plus, în baza continuităţii funcţiei
r
→
¨
,
{\displaystyle {\ddot {\vec {r}}},\!}
lim
k
→
0
r
→
¨
(
t
k
)
=
r
→
¨
(
t
0
)
.
{\displaystyle \lim _{k\to 0}{\ddot {\vec {r}}}(t_{k})={\ddot {\vec {r}}}(t_{0}).\!}
r
→
(
t
0
+
k
)
−
r
→
(
t
0
)
k
=
r
→
˙
(
t
0
)
+
k
2
!
⋅
r
→
¨
(
t
k
)
.
{\displaystyle {\frac {{\vec {r}}(t_{0}+k)-{\vec {r}}(t_{0})}{k}}={\dot {\vec {r}}}(t_{0})+{\frac {k}{2!}}\cdot {\ddot {\vec {r}}}(t_{k}).\!}
M
0
M
0
′
→
,
{\displaystyle {\overrightarrow {M_{0}M'_{0}}},\!}
r
→
¨
(
t
k
)
{\displaystyle {\ddot {\vec {r}}}(t_{k})\!}
k .
Trecând la limită pentru
k
→
0
,
{\displaystyle k\to 0,\!}
r
→
¨
(
t
0
)
{\displaystyle {\ddot {\vec {r}}}(t_{0})\!}
r
→
˙
(
t
0
)
{\displaystyle {\dot {\vec {r}}}(t_{0})\!}
r
→
¨
(
t
0
)
.
{\displaystyle {\ddot {\vec {r}}}(t_{0}).\!}
P
M
0
o
(
Γ
)
:
(
R
→
−
r
→
(
t
0
)
;
r
→
˙
(
t
0
)
;
r
→
¨
(
t
0
)
)
=
0
{\displaystyle P_{M_{0}}^{o}(\Gamma ):\;({\vec {R}}-{\vec {r}}(t_{0});{\dot {\vec {r}}}(t_{0});{\ddot {\vec {r}}}(t_{0}))=0\!}
iar ecuaţia carteziană a planului osculator este:
P
M
0
O
(
Γ
)
:
|
X
−
x
(
t
0
)
Y
−
y
(
t
0
)
Z
−
z
(
t
0
)
x
˙
(
t
0
)
y
˙
(
t
0
)
z
˙
(
t
0
)
x
¨
(
t
0
)
y
¨
(
t
0
)
z
¨
(
t
0
)
|
=
0
{\displaystyle P_{M_{0}}^{O}(\Gamma ):\;{\begin{vmatrix}X-x(t_{0})&Y-y(t_{0})&Z-z(t_{0})\\{\dot {x}}(t_{0})&{\dot {y}}(t_{0})&{\dot {z}}(t_{0})\\{\ddot {x}}(t_{0})&{\ddot {y}}(t_{0})&{\ddot {z}}(t_{0})\end{vmatrix}}=0\!}
Γ
{\displaystyle \Gamma \!}
P
M
0
O
(
Γ
)
:
{
X
=
x
(
t
0
)
+
α
x
˙
(
t
0
)
+
β
x
¨
(
t
0
)
Y
=
y
(
t
0
)
+
α
y
˙
(
t
0
)
+
β
y
¨
(
t
0
)
Z
=
z
(
t
0
)
+
α
z
˙
(
t
0
)
+
β
z
¨
(
t
0
)
{\displaystyle P_{M_{0}}^{O}(\Gamma ):{\begin{cases}X=x(t_{0})+\alpha {\dot {x}}(t_{0})+\beta {\ddot {x}}(t_{0})\\Y=y(t_{0})+\alpha {\dot {y}}(t_{0})+\beta {\ddot {y}}(t_{0})\\Z=z(t_{0})+\alpha {\dot {z}}(t_{0})+\beta {\ddot {z}}(t_{0})\end{cases}}\!}
α
,
β
{\displaystyle \alpha , \beta \!}
sau
P
M
0
O
(
Γ
)
:
A
[
x
−
x
(
t
0
)
]
+
B
[
y
−
y
(
t
0
)
]
+
C
[
z
−
z
(
t
0
)
]
=
0
{\displaystyle P_{M_{0}}^{O}(\Gamma ):\;A[x-x(t_{0})]+B[y-y(t_{0})]+C[z-z(t_{0})]=0\!}
A
,
B
,
C
{\displaystyle A, B, C \!}
matricei :
[
x
˙
(
t
0
)
y
˙
(
t
0
)
z
˙
(
t
0
)
x
¨
(
t
0
)
y
¨
(
t
0
)
z
¨
(
t
0
)
]
{\displaystyle {\begin{bmatrix}{\dot {x}}(t_{0})&{\dot {y}}(t_{0})&{\dot {z}}(t_{0})\\{\ddot {x}}(t_{0})&{\ddot {y}}(t_{0})&{\ddot {z}}(t_{0})\end{bmatrix}}\!}
Observaţii .
1 .
Planul osculator al unei curbe plane este chiar planul curbei.
2 .
Direcţia normală a planului osculator
P
M
0
O
(
Γ
)
{\displaystyle P_{M_{0}}^{O}(\Gamma )\!}
[
i
→
j
→
k
→
x
˙
(
t
0
)
y
˙
(
t
0
)
z
˙
(
t
0
)
x
¨
(
t
0
)
y
¨
(
t
0
)
z
¨
(
t
0
)
]
=
A
i
→
+
B
j
→
+
C
k
→
.
{\displaystyle {\begin{bmatrix}{\vec {i}}&{\vec {j}}&{\vec {k}}\\{\dot {x}}(t_{0})&{\dot {y}}(t_{0})&{\dot {z}}(t_{0})\\{\ddot {x}}(t_{0})&{\ddot {y}}(t_{0})&{\ddot {z}}(t_{0})\end{bmatrix}}=A{\vec {i}}+B{\vec {j}}+C{\vec {k}}.\!}
Dreapta normală pe planul osculator (adică dreapta de direcţie
(
→
˙
t
0
)
×
(
→
¨
t
0
)
{\displaystyle {\dot {\vec {(}}}t_{0})\times {\ddot {\vec {(}}}t_{0})\!}
M
0
{\displaystyle M_0 \!}
binormală , şi se notează cu
B
M
0
(
Γ
)
.
{\displaystyle B_{M_{0}}(\Gamma ).\!}

















![{\displaystyle {\frac {1}{k}}[{\vec {r}}(t_{0}+k)-{\vec {r}}(t_{0})]\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/5d73d767f623ebd2dd3673653b7ffc8b9d27a6f8)




















![{\displaystyle P_{M_{0}}^{O}(\Gamma ):\;A[x-x(t_{0})]+B[y-y(t_{0})]+C[z-z(t_{0})]=0\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/e66523eb558de24fb8640b8e5fa7470013a4cc18)






