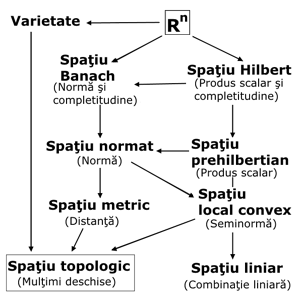
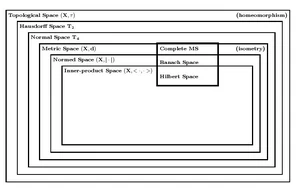
Spaţiile abstracte ale matematicii superioare. Săgeata indică incluziunea: Mulţimile din originea săgeţii sunt incluse în cele din vârf.
Definiție [ ] DEFINIȚIA 1 .
Se numește spațiu vectorial sau spațiu liniar peste un corp K , o mulțime nevidă V dotată cu două operații,
+
:
V
×
V
→
V
{\displaystyle +: V \times V \rightarrow V \!}
⋅
:
K
×
V
→
V
,
{\displaystyle \cdot : K \times V \rightarrow V, \!}
I .
(
V
,
+
)
{\displaystyle (V, +) \!}
grup abelian adică posedă proprietăţile:
a)
(
u
+
v
)
+
w
=
u
+
(
v
+
w
)
,
∀
u
,
v
,
w
∈
V
{\displaystyle (u+v)+w = u+ (v+w), \; \forall u,v,w \in V }
b)
∃
0
V
∈
V
,
{\displaystyle \exists 0_V \in V, }
u
+
0
V
=
0
V
+
u
,
∀
u
∈
V
{\displaystyle u+ 0_V = 0_V+ u, \; \forall u \in V }
c)
∀
u
∈
V
,
∃
(
−
u
)
∈
V
{\displaystyle \forall u \in V , \; \exists (-u) \in V }
u
+
(
−
u
)
=
(
−
u
)
+
u
=
0
V
{\displaystyle u+ (-u) = (-u)+u=0_V }
d)
u
+
v
=
v
+
u
,
∀
u
,
v
∈
V
{\displaystyle u+v= v+u, \; \forall u,v \in V }
II . a)
(
α
+
β
)
⋅
x
=
α
⋅
x
+
β
⋅
x
,
∀
α
,
β
∈
K
,
∀
x
∈
V
;
{\displaystyle (\alpha + \beta) \cdot x = \alpha \cdot x + \beta \cdot x, \; \forall \alpha, \beta \in K, \; \forall x \in V; \!}
b)
α
⋅
(
x
+
y
)
=
α
⋅
x
+
α
⋅
y
,
∀
α
∈
K
,
∀
x
,
y
∈
V
;
{\displaystyle \alpha \cdot (x+y) = \alpha \cdot x + \alpha \cdot y, \; \forall \alpha \in K, \; \forall x, y \in V; \!}
c)
(
α
β
)
⋅
x
=
α
⋅
(
β
⋅
x
)
,
∀
α
,
β
∈
K
,
∀
x
∈
V
;
{\displaystyle (\alpha \beta) \cdot x = \alpha \cdot (\beta \cdot x), \; \forall \alpha, \beta \in K, \; \forall x \in V; \!}
d)
1
K
⋅
x
=
x
,
∀
x
∈
V
,
{\displaystyle 1_K \cdot x=x, \; \forall x \in V, \!}
1
K
{\displaystyle 1_K \!}
K . Elementele lui
K
{\displaystyle K}
scalari , iar ale lui
V
{\displaystyle V}
vectori .
Exemple de spații vectoriale [ ]
∙
(
R
n
,
R
)
{\displaystyle \bullet \; \; (\mathbb R^n, \mathbb R) \!}
spațiul vectorial numeric real n-dimensional , unde
R
n
=
{
(
x
1
,
x
2
,
⋯
,
x
n
)
|
x
i
∈
R
,
i
=
1
,
n
¯
}
.
{\displaystyle \mathbb R^n = \{ (x_1, x_2, \cdots , x_n) \; | \; x_i \in \mathbb R, i=\overline {1, n} \}. \!}
∙
(
M
m
,
n
(
R
)
,
R
)
{\displaystyle \bullet \; \; (M_{m,n}(\mathbb R), \mathbb R) \!}
spațiul vectorial real al matricelor de tipul
(
m
,
n
)
{\displaystyle (m,n) \!}
numere reale .
∙
(
R
[
X
]
,
R
)
{\displaystyle \bullet \; \; (\mathbb R[X], \mathbb R) \!}
spațiul vectorial real al polinoamelor în nedeterminata X , cu coeficienți reali.
∙
(
R
[
X
]
,
R
)
{\displaystyle \bullet \; \; (\mathbb R[X], \mathbb R) \!}
spațiul vectorial real al funcțiilor de grad cel mult n , în nedeterminata X , cu coeficienți reali.
∙
(
F
[
a
,
b
]
,
R
)
{\displaystyle \bullet \; \; ( F[a, b], \mathbb R) \!}
spațiul vectorial real al funcțiilor reale definite pe intervalul
[
a
,
b
]
.
{\displaystyle [a, b]. \!}
∙
{\displaystyle \bullet \!}
ecuații diferențiale liniare omogene
∙
{\displaystyle \bullet \!}
seriilor convergente formează un spațiu vectorial.
DEFINIȚIA 2 .
Fie
(
V
,
K
)
{\displaystyle (V, K) \!}
W
⊂
V
,
W
≠
∅
.
{\displaystyle W \subset V, \; W \neq \empty. \!}
W este subspațiu vectorial al spațiului vectorial
(
V
,
K
)
{\displaystyle (V, K) \!}
1)
∀
x
,
y
∈
W
⇒
x
+
y
∈
W
;
{\displaystyle \forall \; x, y \in W \; \Rightarrow \; x+y \in W; \!}
2)
∀
α
∈
K
,
x
∈
W
⇒
α
⋅
x
∈
W
.
{\displaystyle \forall \; \alpha \in K, x \in W \; \Rightarrow \; \alpha \cdot x \in W. \!}
OBSERVAȚIE.
Un subspațiu vectorial are o structură de spațiu vectorial în raport cu operațiile induse.
EXEMPLUL 1 .
Considerăm operațiile:
⊕
:
R
+
∗
×
R
+
∗
→
R
+
∗
{\displaystyle \oplus : \mathbb R_+^* \times \mathbb R^*_+ \rightarrow \mathbb R^*_+ \!}
⊗
:
R
+
∗
×
R
+
∗
→
R
+
∗
,
{\displaystyle \otimes : \mathbb R_+^* \times \mathbb R^*_+ \rightarrow \mathbb R^*_+, \!}
x
⊕
y
=
x
⋅
y
,
α
⊗
x
=
x
α
,
∀
x
,
y
∈
R
+
∗
,
∀
α
∈
R
,
{\displaystyle x \oplus y = x \cdot y, \; \alpha \otimes x = x^{\alpha}, \; \forall \; x, y \in \mathbb R^*_+, \forall \; \alpha \in \mathbb R, \!}
unde "
⋅
{\displaystyle \cdot \!}
Să arătăm că
R
+
∗
{\displaystyle \mathbb R^*_+ \!}
Verificăm condițiile din definiția 1:
I. a) Fie
x
,
y
∈
R
+
∗
;
{\displaystyle x, y \in \mathbb R^*_+; \!}
x
⊕
y
=
x
⋅
y
=
y
⋅
x
=
y
⊕
x
,
{\displaystyle x \oplus y = x \cdot y = y \cdot x = y \oplus x, \!}
b) Fie
x
,
y
,
z
∈
R
+
∗
;
{\displaystyle x, y, z \in \mathbb R^*_+; \!}
(
x
⊕
y
)
⊕
z
=
(
x
⋅
y
)
⋅
z
=
x
⋅
(
y
⋅
z
)
=
x
⊕
(
y
⊕
z
)
,
{\displaystyle (x \oplus y) \oplus z = (x \cdot y) \cdot z = x \cdot (y \cdot z) = x \oplus (y \oplus z), \!}
în baza asociativității înmulțirii numerelor reale.
c) Numărul real 1 este elementul neutru față de operația
⊕
:
{\displaystyle \oplus: \!}
x
⊕
1
=
1
⊕
x
=
x
,
∀
x
∈
R
+
∗
.
{\displaystyle x \oplus 1 = 1 \oplus x = x, \; \forall \; x \in \mathbb R^*_+. \!}
d)
∀
x
∈
R
+
∗
,
∃
x
−
1
=
1
x
∈
R
+
∗
{\displaystyle \forall \; x \in \mathbb R^*_+, \; \exists x^{-1} = \frac 1 x \in \mathbb R^*_+ \!}
x
⊕
x
−
1
=
x
−
1
⊕
x
=
x
⋅
1
x
=
1.
{\displaystyle x \oplus x^{-1} = x^{-1} \oplus x = x \cdot \frac 1 x = 1. \!}
II. a) Fie
α
,
β
∈
R
,
x
∈
R
+
∗
.
{\displaystyle \alpha, \beta \in \mathbb R, \; x \in \mathbb R^*_+. \!}
(
α
+
β
)
⊗
x
=
x
α
+
β
=
x
α
⋅
x
β
=
α
⊗
x
⊕
β
⊗
x
.
{\displaystyle (\alpha + \beta) \otimes x = x^{\alpha + \beta} = x^{\alpha} \cdot x^{\beta} = \alpha \otimes x \oplus \beta \otimes x. \!}
b) Fie
α
∈
R
,
x
,
y
∈
R
+
∗
.
{\displaystyle \alpha \in \mathbb R, \; x, y \in \mathbb R^*_+. \!}
α
⊗
(
x
⊕
y
)
=
(
x
⊕
y
)
α
=
(
x
⋅
y
)
α
=
x
α
⋅
y
α
=
(
α
⊗
x
)
⊕
(
α
⊗
y
)
.
{\displaystyle \alpha \otimes (x \oplus y) = (x \oplus y)^{\alpha} = (x \cdot y)^{\alpha} = x^{\alpha} \cdot y^{\alpha} = (\alpha \otimes x) \oplus (\alpha \otimes y). \!}
c) Fie
α
,
β
∈
R
,
x
∈
R
+
∗
.
{\displaystyle \alpha, \beta \in \mathbb R, \; x \in \mathbb R^*_+. \!}
(
α
β
)
⊗
x
=
x
α
β
=
x
β
α
=
(
x
β
)
α
=
α
⊗
(
x
β
)
=
α
⊗
(
β
⊗
x
)
.
{\displaystyle (\alpha \beta) \otimes x = x^{\alpha \beta} = x^{\beta \alpha}= (x^{\beta})^{\alpha} = \alpha \otimes (x^{\beta}) = \alpha \otimes (\beta \otimes x) . \!}
d) Fie
x
∈
R
+
∗
;
{\displaystyle x \in \mathbb R^*_+; \!}
1
R
⊗
x
=
x
1
=
x
.
{\displaystyle 1_R \otimes x = x^1 = x. \!}
Conform definiției 1, din I și II rezultă că
R
+
∗
{\displaystyle \mathbb R^*_+ \!}
EXEMPLUL 2 .
Mulțimea:
V
=
{
(
x
1
,
x
2
,
⋯
,
x
n
)
t
|
x
i
∈
R
,
i
=
1
,
n
¯
,
x
1
+
x
n
−
1
=
0
}
,
{\displaystyle V = \{ (x_1, x_2, \cdots , x_n)^t \; | \; x_i \in \mathbb R, \; i= \overline {1, n}, \; x_1+x_{n-1} = 0 \}, \!}
împreună cu adunarea vectorilor din
R
n
{\displaystyle \mathbb R^n \!}
Demonstrație :Deoarece
V
⊂
R
n
{\displaystyle V \subset \mathbb R^n \!}
(
R
n
,
R
)
{\displaystyle (\mathbb R^n, \mathbb R) \!}
V este un subspațiu al spațiului
(
R
n
,
R
)
.
{\displaystyle (\mathbb R^n, \mathbb R). \!}
1) Fie
x
,
y
∈
V
.
{\displaystyle x, y \in V. \!}
x
=
(
x
1
,
x
2
,
⋯
,
x
n
)
t
,
x
i
,
i
=
1
,
n
¯
,
{\displaystyle x = (x_1, x_2, \cdots , x_n)^t, \; x_i, \; i= \overline {1, n}, \!}
x
n
+
x
n
+
1
=
0
{\displaystyle x_n + x_{n+1} = 0 \!}
y
=
(
y
1
,
y
2
,
⋯
,
y
n
)
t
,
y
i
∈
R
,
i
=
1
,
n
¯
{\displaystyle y= (y_1, y_2, \cdots , y_n)^t, \; y_i \in \mathbb R, \; i = \overline {1, n} \!}
y
1
+
y
n
−
1
=
0.
{\displaystyle y_1+y_{n-1} = 0. \!}
x
+
y
=
(
x
1
+
y
1
,
x
2
+
y
2
,
⋯
,
x
n
+
y
n
)
t
,
x
i
+
y
i
∈
R
,
i
=
1
,
n
¯
,
{\displaystyle x+y = (x_1 + y_1, x_2+ y_2, \cdots , x_n + y_n)^t, \; x_i+y_i \in \mathbb R, \; i = \overline {1, n}, \!}
(
x
+
y
)
1
+
(
x
+
y
)
n
−
1
=
x
1
+
y
1
+
x
n
−
1
+
y
n
−
1
=
0
,
{\displaystyle (x+y)_1 + (x+y)_{n-1} = x_1 + y_1 + x_{n-1} + y_{n-1}=0, \!}
x
+
y
∈
V
.
{\displaystyle x+y \in V. \!}
2) Fie
α
∈
R
,
x
∈
V
.
{\displaystyle \alpha \in \mathbb R, \; x \in V. \!}
α
x
=
(
α
x
1
,
α
x
2
,
⋯
,
α
x
n
)
t
,
α
x
i
∈
R
,
i
=
1
,
n
¯
,
{\displaystyle \alpha x = (\alpha x_1, \alpha x_2, \cdots , \alpha x_n)^t, \; \alpha x_i \in \mathbb R, \; i= \overline {1, n}, \!}
(
α
x
)
1
+
(
α
x
)
n
−
1
=
α
(
x
1
+
x
n
−
1
)
=
0
,
{\displaystyle (\alpha x)_1 + (\alpha x)_{n-1} = \alpha (x_1 + x_{n-1}) =0, \!}
α
x
∈
V
.
{\displaystyle \alpha x \in V. \!}
Conform definiției 2, din 1) și 2) rezultă că V este un subspațiu vectorial al spațiului
(
R
n
,
R
)
,
{\displaystyle (\mathbb R^n, \mathbb R), \!}
V este un spațiu vectorial real.
Probleme propuse [ ] 1 . Să se arate că mulțimea:
C
[
a
,
b
]
=
{
f
|
f
:
[
a
,
b
]
→
R
,
{\displaystyle \mathcal C_{[a,b]} = \{ f \; | \; f: [a,b] \rightarrow \mathbb R, \; }
f continuă pe
[
a
,
b
]
}
,
{\displaystyle [a, b] \}, \!}
R
.
{\displaystyle \mathbb R. \!}
2 . Să se arate că mulțimea
M
m
,
n
(
R
)
{\displaystyle M_{m,n}(\mathbb R) \!}
m linii și n coloane și elemente numere reale are o structură de spațiu vectorial real în raport cu operațiile de adunare a matricelor și de înmulțire a acestora cu scalari reali.
3 . Să se arate că mulțimea:
A
=
{
(
0
a
b
c
0
d
)
;
a
,
b
,
c
,
d
∈
R
,
c
=
a
+
b
}
{\displaystyle A = \left \{ \begin{pmatrix} 0 & a & b \\ c & 0 & d \end{pmatrix}; \; a, b, c, d \in \mathbb R, \; c=a+b \right \} \!}
împreună cu operațiile de adunare a matricelor și de înmulțire a acestora cu scalari reali formează un spațiu vectorial peste
R
.
{\displaystyle \mathbb R. \!}
4 . Considerăm operațiile:
⊕
:
(
R
+
∗
)
2
×
(
R
+
∗
)
2
→
(
R
+
∗
)
2
{\displaystyle \oplus : (\mathbb R^*_+)^2 \times (\mathbb R^*_+)^2 \rightarrow (\mathbb R^*_+)^2 \!}
și
⊗
:
(
R
+
∗
)
2
×
(
R
+
∗
)
2
→
(
R
+
∗
)
2
,
{\displaystyle \otimes : (\mathbb R^*_+)^2 \times (\mathbb R^*_+)^2 \rightarrow (\mathbb R^*_+)^2, \!}
cu
(
x
1
,
x
2
)
⊕
(
y
1
,
y
2
)
=
(
x
1
⋅
y
1
,
x
2
⋅
y
2
)
,
{\displaystyle (x_1, x_2) \oplus (y_1, y_2) = (x_1 \cdot y_1, x_2 \cdot y_2), \!}
α
⊗
(
x
1
,
x
2
)
=
(
x
1
α
,
x
2
α
)
,
∀
x
,
y
∈
R
+
∗
,
∀
α
∈
R
.
{\displaystyle \alpha \otimes (x_1, x_2)= (x^{\alpha}_1, x^{\alpha}_2), \; \forall \; x, y \in \mathbb R^*_+, \; \forall \; \alpha \in \mathbb R. \!}
Să se studieze dacă
(
R
+
∗
)
2
{\displaystyle (\mathbb R^*_+)^2 \!}
5 . Să se arate că mulțimea:
A
=
{
(
a
¯
b
¯
b
a
)
;
a
,
b
∈
C
}
{\displaystyle A = \left \{ \begin{pmatrix} \overline a & \overline b \\ b & a \end{pmatrix}; \; a, b \in \mathbb C \right \} \!}
(unde
a
¯
{\displaystyle \overline a \!}
numărului complex a ), împreună cu operațiile de adunare a matricelor și de înmulțire a acestora cu scalari reali formează un spațiu vectorial peste
C
.
{\displaystyle \mathbb C. \!}
6 . Să se arate că următoarele mulțimi sunt subspații vectoriale ale spațiilor vectoriale indicate:a)
R
n
[
X
]
⊂
R
[
X
]
;
{\displaystyle \mathbb R_n[X] \subset \mathbb R[X]; \!}
b)
{
(
a
,
0
,
b
)
t
|
a
,
b
∈
R
}
⊂
R
3
;
{\displaystyle \left \{ (a, 0, b)^t \; | \; a, b \in \mathbb R \right \} \subset \mathbb R^3; \!}
c)
{
2
a
X
5
+
b
X
2
|
a
,
b
∈
R
}
⊂
R
[
X
]
;
{\displaystyle \left \{ 2a X^5 + b X^2 \; | \; a, b \in \mathbb R \right \} \subset \mathbb R[X]; \!}
d)
{
(
x
1
,
x
2
,
x
3
)
t
|
x
i
∈
R
,
i
=
1
,
3
¯
,
x
1
=
3
x
2
,
x
1
+
x
2
=
x
3
}
⊂
R
3
.
{\displaystyle \left \{ (x_1, x_2, x_3)^t \; | \; x_i \in \mathbb R, \; i= \overline {1, 3}, \; x_1 = 3 x_2, \; x_1 + x_2 = x_3 \right \} \subset \mathbb R^3. \!}
Vezi și [ ]
Resurse [ ] 




















![{\displaystyle \bullet \;\;(\mathbb {R} [X],\mathbb {R} )\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/a0de55daaeba1fb9ab88cc61538d5d67533a507a)
![{\displaystyle \bullet \;\;(F[a,b],\mathbb {R} )\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/dd388a3bea0987219132e14cba225a6c0fb34372)
![{\displaystyle [a,b].\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/89810b82fa1649213d6d00bc1128b5e0cdf47807)











































![{\displaystyle {\mathcal {C}}_{[a,b]}=\{f\;|\;f:[a,b]\rightarrow \mathbb {R} ,\;}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/25b7370e96ece1d8f832bc3bd6b549b79ff12482)
![{\displaystyle [a,b]\},\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/e61a681412193d7f2c76a28ddf6a0af1808810fd)











![{\displaystyle \mathbb {R} _{n}[X]\subset \mathbb {R} [X];\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/fc5bdf0692dc1ec5984db07599a3607ce101dc73)

![{\displaystyle \left\{2aX^{5}+bX^{2}\;|\;a,b\in \mathbb {R} \right\}\subset \mathbb {R} [X];\!}](https://services.fandom.com/mathoid-facade/v1/media/math/render/svg/044bebd93df1c4fcfe5cba9db3899fe11041f72f)
