Axiomele geometriei

Euclid, autorul Elementelor şi al axiomei care îi poartă numele.

Axiomele geometriei în plan şi în spaţiu

Cunoştinţele de geometrie acumulate în clasele gimnaziale pot fi încadrate într-un sistem logic de propoziţii matematice: axiome, definiţii, teoreme, consecinţe, leme, etc. Amintim că noţiunile geometrice ce nu se definesc se numesc noţiuni geometrice primare. De regulă, acestea sînt: punct, dreaptă, plan. Punctele, dreptele şi planele se notează respectiv cu literele $A , B , C , ...; a , b , c , ...; \alpha, \beta, \gamma , ...$eventual cu indici. Noţiunile ce se definesc cu ajutorul noţiunilor primare se numesc noţiuni derivate. Segment, semidreaptă, unghi, triunghi, ş. a. sînt noţiuni derivate. Punctele, dreptele şi planele se află în nişte relaţii numite relaţii primare. Acestea se numesc „incidenţă” (apartenenţă), „între”, „congruenţă”. Natura obiectelor primare (punct, dreaptă, plan) şi a relaţiilor primare poate fi arbitrară cu condiţia că ele sînt legate printr-un sistem de axiome.

Axiomele sînt propoziţii cu caracter de ipoteză (care nu se demonstrează) care descriu legătura dintre noţiunile primare şi relaţiile primare. Ele reprezintă proprietăţile de bază ale obiectelor de bază şi se consideră adevărate. Axiomele sunt ca nişte reguli de conduită, ca nişte reguli ale unui joc, ş. a. Sistemul de axiome (reguli) ales trebuie să verifice următoarele condiţii:

• axiomele trebuie să nu se contrazică;

• axiomele să fie suficient de numeroase, astfel încât pornind de la ele să se poată studia, explica toate situaţiile posibile.

În geometria elementară se iau ca axiome proprietăţi ale punctelor şi dreptelor deja familiarizate şi amplu utilizate în gimnaziu. La ele se mai adaugă şi alte cîteva proprietăţi importante sugerate de observaţii şi experimentări. Menţionăm că una şi aceeaşi proprietate poate fi considerată într-un sistem de proprietăţi drept axiomă, iar în alt sistem de axiome drept o consecinţă din axiomele acceptate, adică drept teoremă.

Axiomele sînt propoziţii cu caracter de ipoteză (care nu se demonstrează) care descriu legătura dintre noţiunile primare şi relaţiile primare. Teorema este o propoziţie adevărul căreia se demonstrează. Teoremele sunt propoziţii care descriu proprietăţile noţiunilor primare şi derivate şi se demonstrează cu ajutorul axiomelor, definiţiilor, lemelor sau teoremelor deja demonstrate. Lema este o propoziţie adevărul căreia se demonstrează şi se aplică la demonstrarea unei teoreme.

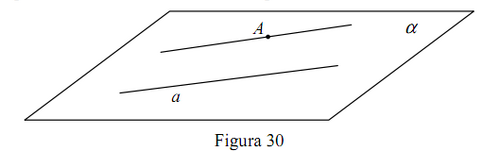
Definiţia este o propoziţie sau un grup de propoziţii prin care se explică o noţiune nouă. Astfel, propoziţia „Dacă două puncte A şi B ale dreptei a aparţin planului α , atunci dreapta a aparţine planului α ” este o axiomă (după cum vom vedea), iar afirmaţia „Suma măsurilor unghiurilor unui triunghi este 180°” este o teoremă. Această teoremă se demonstrează cu ajutorul următoarelor propoziţii matematice:

P1. axioma paralelelor a lui Euclid (oricare ar fi o dreaptă şi un punct exterior acestei drepte, în planul determinat de punct şi dreaptă, există cel mult o paralelă la dreapta dată, care să conţină punctul dat);

P2. teorema de existenţă a paralelei (printr-un punct exterior unei drepte există cel puţin o paralelă la dreapta dată);

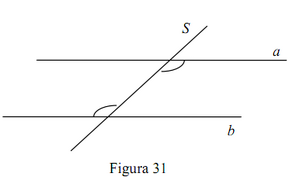
P3. teorema despre egalitatea unghiurilor alterne interne, formate la intersecţia a două drepte paralele cu o secantă;

P4. definiţia sumei unghiurilor;

P5. definiţia unghiului alungit;

P6. teorema despre măsura unghiului alungit.

Convenim ca atunci când ne referim la mai multe obiecte (puncte, drepte, plane, ş.a.) şi le notăm cu simboluri diferite, să le considerăm distincte. Iată câteva exemple de definiţii care vor fi folosite în continuare: Trei puncte $A, B, C \!$ se numesc coliniare dacă există o dreaptă a ce le conţine. În caz contrar, punctele se numesc necoliniare. Se spune că dreapta $a \!$ intersectează (este incidentă cu) planul $\alpha \!$ dacă există un punct A , astfel încât $A \in \alpha \!$ şi $A \in a. \!$ Se spune că dreapta $a \!$ aparţine (sau este conţinută de planul $\alpha \!$) planului $\alpha \!$ dacă orice punct al dreptei a aparţine şi planului $\alpha. \!$ Patru puncte $A, B, C, D \!$ se numesc coplanare dacă există un plan α ce le conţine. În caz contrar, punctele sunt necoplanare.

Alegerea noţiunilor primare, relaţiilor primare şi a sistemului de axiome respectiv, astfel încât toată geometria elementară să fie dedusă bazându-ne doar pe ele şi pe legile logicii se numeşte construcţie axiomatică a geometriei elementare. Se cunosc mai multe sisteme de axiome ale geometriei elementare. În literatura ştiinţifică este cel mai des utilizat sistemul de axiome al lui D. Hilbert. Geometria organizată conform acestui sistem de axiome corespunde cu geometria spaţiului din jurul nostru, observată cu „ochiul liber”. Conform acestei geometrii, oamenii activează în diversele lor meserii, de exemplu, în arhitectură, construcţia de poduri, construcţia de case, de maşini, ş. a. În afară de această geometrie matematică au mai fost definite şi alte geometrii, bazate pe alte axiome, unele din ele contrazic axiomele geometriei elementare. Aceste geometrii sînt utile în explicarea şi prezicerea fenomenelor ce se petrec în Univers: teoria relativităţii, evoluţia stelelor, propagarea luminii, ş. a.

În continuare vom examina schema argumentării geometriei elementare conform axiomaticii lui David Hilbert. Acest sistem de axiome constă din 20 de axiome împărţite în 5 grupe. Prin această clasificare a axiomelor se reuşeşte cea mai simplă şi laconică formulare a axiomelor şi în plus, se poate constata cât de consistentă (bogată) poate fi geometria bazată doar pe una sau câteva grupe de axiome.

Axiomele de incidenţă (Grupa I)

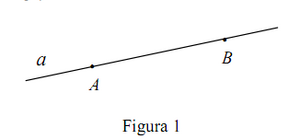
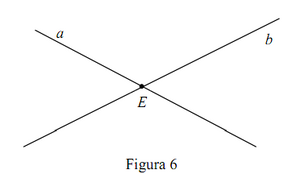
Axiomele acestei grupe definesc proprietăţile de amplasare ale punctelor, dreptelor şi planelor. Se admit următoarele axiome de incidenţă: I1. Oricare ar fi două puncte distincte A , B ale spaţiului, există o dreaptă a care trece prin aceste puncte. I2. Oricare ar fi două puncte distincte A , B există cel mult o dreaptă a care trece prin aceste puncte. Deci, două puncte distincte A , B ale spaţiului determină o dreaptă şi numai una singură. Notaţie: a = AB (fig. 1).

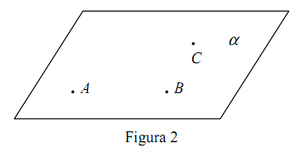
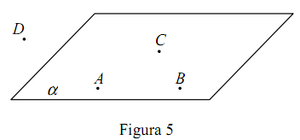
I3. Pe oricare dreaptă sînt situate cel puţin două puncte. Există cel puţin trei puncte necoliniare. I4. Oricar ar fi trei puncte necoliniare A , B , C , există planul α ce trece prin aceste puncte. Pe fiecare plan este situat cel puţin un punct. I5. Oricare ar fi trei puncte necoliniare A , B , C , există cel mult un plan α care trece prin aceste puncte. Astfel, trei puncte necoliniare A , B , C , determină un plan α şi numai unul singur. Notaţie: α = (ABC) (fig. 2).

I6. Dacă două puncte distincte A , B ale dreptei a sunt situate pe planul α, atunci fiecare punct al dreptei a este situat pe planul α . Altfel spus, dacă o dreaptă are două puncte comune cu un plan, atunci dreapta este conţinută în întregime în acest plan.

I7. Dacă două plane α şi β au un punct comun A , atunci ele mai au cel puţin încă un punct comun B . Planele se reprezintă pe foaie de caiet prin paralelograme.

I8. Exista cel putin patru puncte necoliniare.

Utilizand aceste axiome pot fi demonstrate urmatoarele teoreme:

T1. Două drepte distincte au cel mult un punct comun.

T2. Dacă două plane au un punct comun, atunci ele au o dreaptă comună pe care sînt situate toate punctele comune acestor plane.

T3. Printr-o dreaptă şi un punct ce nu-i aparţine trece un plan şi numai unul singur.

T4. Prin două drepte concurente trece un plan şi numai unul singur.

T5. Orice plan conţine trei puncte necoliniare.

Aşadar, un plan poate fi determinat:

a) de trei puncte necoliniare,

b) de o dreaptă şi un punct ce nu-i aparţine,

c) de două drepte secante (care se intersectează).

Să demonstrăm de exemplu teoremele 3 şi 4.

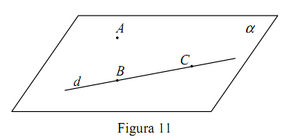
Teorema 3. Printr-o dreaptă şi un punct ce nu aparţine acestei drepte trece un unic plan.

Demonstraţie. Fie dreapta d dată şi punctul A ∉ d . Conform axiomei I3 pe dreapta d există două puncte distincte B şi C (fig. 11). Punctele A , B , C sînt necoliniare, deci, conform axiomelor I4-I5, prin aceste puncte trece un plan α şi numai unul singur. Dreapta d aparţine planului α , deoarece două puncte distincte ale ei, B şi C , aparţin planului α (axioma I6). Deci, planul α este singurul plan ce conţine punctul A şi dreapta d . ► Acest plan se notează ) (A, d sau ) (d , A . Planul ce trece prin punctele necoliniare A , B , C se notează ) (ABC .

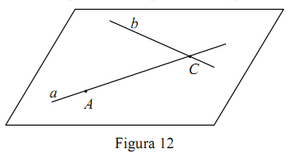
Teorema 4. Există un unic plan ce trece prin două drepte concurente.

Demonstraţie. Fie a şi b două drepte concurente în C . Pe dreapta a , în afară de punctul C mai există cel puţin un punct A, (fig. 12). Conform teoremei 3, prin A ≠ C punctul A şi dreapta b trece un plan α şi numai unul singur. Unicitatea planului rezultă din axioma I6, deoarece orice punct al dreptei AC aparţine planului α . ► Exerciţiu. Demonstraţi teoremele T1, T2, T5.

Axiomele de ordine (grupa II)

Axiomele de ordine evidenţiază relaţia dintre punctele situate pe o dreaptă; această relaţie se exprimă prin cuvintele „a fi între” şi altele echivalente cu acestea. Dacă punctul B este situat (se află) între punctele A şi C notăm A − B − C .

Se admit următoarele axiome de ordine:

$II_1. \!$ Dacă avem A − B − C , atunci A , B , C sînt puncte distincte coliniare şi avem C − B − A.

$II_2. \!$ (Axioma punctului exterior). Oricare ar fi două puncte distincte A , B există cel puţin un punct C astfel încât A − B − C.

$II_3. \!$ Oricare ar fi trei puncte distincte coliniare A , B , C , unul şi numai unul este situat între celelalte două.

Înainte de a formula axioma II4 definim noţiunile de segment şi triunghi. Figura ce constă din două puncte distincte A , B şi mulţimea tuturor punctelor dreptei AB situate între A şi B se numeşte segment închis determinat de punctele A, B şi se notează [AB]:

$[AB] = \{A, B \} \cup \{ M \in AB | A - M - B \}. \!$

Punctele A şi B se numesc capetele (extremităţile) segmentului. Uneori se spune că segmentul AB uneşte punctele A şi B . Pentru comoditate se examinează şi segmentele nule [AA], [BB]. Punctele segmentului, diferite de capetele lui, se numesc puncte interioare ale acestui segment.

Mulţimea tuturor punctelor interioare ale segmentului AB se numeşte segment deschis şi se notează (AB) . Atât segmentul nenul închis, cât şi segmentul deschis determină o dreaptă, care se numeşte dreapta suport a segmentului respectiv.

Dacă o dreaptă trece printr-un singur punct al unui segment, atunci se spune că dreapta intersectează segmentul sau că segmentul intersectează dreapta. Reuniunea a trei puncte necoliniare şi a segmentelor ce unesc aceste puncte se numeşte triunghi.

Fie A , B , C trei puncte necoliniare. Triunghiul determinat de aceste puncte se notează $\triangle ABC. \!$

$\triangle ABC = [AB] \cup [BC] \cup [CA] \!$

Punctele A , B , C se numesc vârfurile triunghiului ABC , segmentele [AB], [BC], [CA] – laturile triunghiului ABC , iar planul (ABC) – planul triunghiului ABC.

$II_4. \!$ (Axioma lui Pasch). Dacă dreapta a este situată în planul (ABC) al $\triangle ABC \!$ şi nu trece prin nici unul din vârfurile A , B , C ale $\triangle ABC, \!$ dar intersectează o latură a $\triangle ABC \!$ (în interior), atunci dreapta a intersectează încă una şi numai una din laturile $\triangle ABC \!$ (în interior).

Axiomele de incidenţă permit să definim semidreapta, semiplanul şi semispaţiul după cum urmează. Mai întîi se formulează şi se demonstrează teoremele de separare a dreptei, planului şi spaţiului, de către un punct, o dreapta, un plan respectiv.

Teorema S1. Orice punct O al unei drepte d împarte dreapta d în două submulţimi nevide disjuncte de puncte, astfel încât orice două puncte A , B din submulţimi diferite sînt separate de punctul O, iar orice două puncte C, D din aceeaşi submulţime nu sînt separate de punctul O .

Teorema S2. Orice dreaptă d inclusă într-un plan $\alpha \!$ împarte planul $\alpha \!$ în două submulţimi nevide disjuncte de puncte, astfel încât pentru orice două puncte A , B din submulţimi diferite, segmentul [AB] intersectează dreapta d, iar pentru orice două puncte C, D din aceeaşi submulţime segmentul nu intersectează dreapta d.

Teorema S3. Orice plan $\alpha \!$ împarte mulţimea punctelor spaţiului în două submulţimi nevide disjuncte de puncte astfel încât pentru orice două puncte A, B din submulţimi diferite segmentul AB intersectează planul $\alpha \!$, iar pentru orice două puncte C, D din aceeaşi submulţime segmentul CD nu intersectează planul $\alpha. \!$

Fiecare din submulţimile din teorema S1 se numesc semidrepte deschise cu originea în O ale dreptei d (sau cu suportul d ).

Reuniunea semidreptei deschise cu originea ei se numeşte semidreaptă închisă. Notaţie: (OA, [OA respectiv sînt semidrepte deschisă, închisă cu originea în O care conţin punctul A.

Semidreptele diferite cu acelaşi support d şi aceeaşi origine O se numesc semidrepte opuse şi se mai notează prin: $(Od', (Od''.\!$

Fiecare din submulţimile din teorema S3 se numesc semispaţii deschise determinate de planul $\alpha \!$ (cu frontiera $\alpha \!$).

Reuniunea semispaţiului deschis cu frontiera sa se numeşte semispaţiu închis. Notaţie: $( \alpha A \!$, $([ \alpha A \!$ este semispaţiul deschis (închis) cu frontiera , care conţine punctul A .

Semispaţiile diferite cu aceeaşi frontieră se numesc semispaţii opuse.

Reuniunea a două semidrepte închise cu originea comună se numeşte unghi. Fie [OA şi [OB două semidrepte.

Axiomele de congruenţă (grupa III)

Axiomele acestei grupe definesc proprietăţile relaţiilor de congruenţă dintre segmente (unghiuri). Se folosesc notaţiile: $[AB] \equiv [CD] \!$ , $\angle AOB \equiv \angle A'O'B \!$ , care se exprimă prin: segmentul AB (respectiv unghiul AOB ) este congruent cu segmentul CD (respectiv cu unghiul $A'O'B' \!$). Aceste axiome sînt:

$III_1. \!$ Fiind date segmentul $AB \!$ şi semidreapta cu originea în $A' \!$ , există un punct B' situat pe această semidreaptă astfel încât $[AB] \equiv [A' B'] . \!$

$III_2. \!$ Dacă $[AB] \equiv [A' B'] \!$ şi $[AB] \equiv [A''B''] \!$ , atunci $[A' B' ] \equiv [A''B''] \!$ .

$III_3. \!$ Dacă $A - B - C , \; A'- B - C' \!$ , $[AB] \equiv [A' B'] \!$ şi $[BC] \equiv [B'C'] \!$ , atunci $[AC] \equiv [A'C ]' \!$ .

$III_4. \!$ Fie $\angle AOB \!$ , dreapta a şi (O' X ' o semidreapta a dreptei a cu originea în punctul O'. Atunci, în semiplanul α există o unică semidreaptă ' O'Y astfel încât $\angle AOB \equiv \angle X'O'Y' \!$

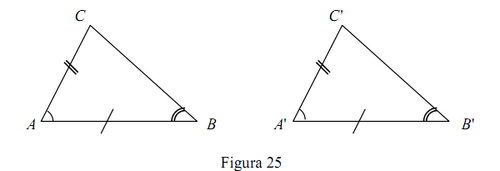
$III_5. \!$ Dacă pentru triunghiurile $ABC \!$ şi $A'B'C' \!$ au loc relaţiile $[AB] \equiv [A'B'], \; [AC] \equiv [A'C'], \; \angle BAC \equiv \angle B'A'C', \!$ atunci are loc relaţia $\angle ABC \equiv \angle A'B'C', \!$ sau, schimbând notaţile, $\angle ACB \equiv \angle A'C'B'. \!$

Aducem ca exemplu câteva teoreme ce rezultă din axiomele de congruenţă şi care le vom utiliza în continuare.

1) Relaţia de congruenţă a segmentelor este o relaţie de echivalenţă pe mulţimea segmentelor.

2) Unghiurile de la baza triunghiului isoscel sînt congruente.

Triunghiurile $ABC \!$ şi $A'B'C' \!$ se numesc congruente dacă există o corespondenţă f între vârfuri, de exemplu $f(A) = A', \; f(B) = B', \; f(C)=C', \!$ astfel încât $\angle A \equiv \angle A', \; \angle B \equiv \angle B', \; \angle C \equiv \angle C', \; [AB] \equiv [A'B'], \; [AC] \equiv [A'C'], \; [BC] \equiv [B'C']. \!$

3) Criteriile de congruenţă ale triunghiurilor:

3a) (Criteriul LUL). Dacă triunghiurile $ABC \!$ şi $A'B'C' \!$ sunt astfel încât $(AB) \equiv (A'B'), \; (AC) \equiv (A'C'), \; \angle A \equiv \angle A', \!$ atunci $\triangle ABC \equiv \triangle A'B'C'. \!$

3b) (Criteriul ULU). Dacă triunghiurile $ABC \!$ şi $A'B'C' \!$ sunt astfel încât $\angle B \equiv \angle B', \; (BC) \equiv (B'C'), \; \angle C \equiv \angle C', \!$ atunci $\triangle ABC \equiv \triangle A'B'C'. \!$

3c) (Criteriul LLL). Dacă triunghiurile $ABC \!$ şi $A'B'C' \!$ sunt astfel încât $(AB) \equiv (A'B'), \; (AC) \equiv (A'C'), \; (BC) \equiv (B'C'), \!$ atunci $\triangle ABC \equiv \triangle A'B'C'. \!$

4) Congruenţa triunghiurilor este o relaţie de echivalenţă pe mulţimea triunghiurilor.

5) Congruenţa unghiurilor este o relaţie de echivalenţă pe mulţimea unghiurilor.

În continuare putem formula definiţiile cunoscute ale noţiunilor "mai mare" şi "mai mic" pentru segmente şi unghiuri şi putem deduce proprietăţile comparaţiei segmentelor şi unghiurilor

De exemplu, spunem că segmentul $(AB) \!$ este mai mic decât segmentul $(CD) \!$ şi scriem $(AB) < (CD) \!$ dacă există un punct E pe semidreapta (CD, astfel încât $C-E-D \!$ şi $(AB) \equiv (CE). \!$

În acest caz se mai spune că $(CD) \!$ este mai mare decât $(AB) \!$ şi se scrie $(CD) > (AB). \!$

Se numesc unghiuri adiacente două unghiuri proprii care au acelaşi vârf, o latură comună şi interioarele disjuncte. ($\angle AOB \!$ şi $\angle AOC \!$).

Două unghiuri adiacente care au laturile necomune opuse se numesc unghiuri suplementare. Un unghi se numeşte drept dacă el este congruent cu suplementarul său.

6) Există un unghi drept.

7) Toate unghiurile drepte sînt congruente între ele.

8) Un unghi exterior al unui triunghi este mai mare decât fiecare dintre unghiurile triunghiului, neadiacent cu acel unghi.

9) În orice triunghi laturii mai mari i se opune un unghi mai mare şi viceversa: unghiului mai mic i se opune latura mai mică.

Axiomele grupelor I-IV permit să dăm definiţia mijlocului unui segment şi a bisectoarei unghiului. Se demonstrează că:

10) Orice segment are un singur mijloc.

11) Orice unghi are o singură bisectoare.

Axiomele de continuitate (grupa IV)

$IV_1 \!$ (Axioma lui Arhimede). Fie segmentele AB şi CD astfel încât $(AB)>(CD). \!$ Atunci pe dreapta AB există un număr finit de puncte $A_1, A_2, \cdots , A_n \!$ astfel încât au loc relaţiile:

a) $A - A_1 - A_2, \; \; A_1-A_2-A_3, \cdots , \; \; A_{n-2}- A_{n-1} - A_n; \!$

b) $(AA_1)= (A_1A_2) = \cdots = (A_{n-1}A_n) = (CD); \!$

c) $A-B- A_n \!$

$IV_2 \!$ Fie pe o dreaptă oarecare a un şir infinit de segmente $(A_1B_1), (A_2B_2), \cdots , (A_nB_n), \cdots \!$ cu proprietăţile:

a) $(A_iB_i) \supset (A_{i+1}B_{i+1}), \; \forall i \in \mathbb N. \!$

b) nu există nici un segment inclus în toate segmentele şirului considerat.

Atunci pe dreapta a există un singur punct M care aparţine fiecărui segment din acest şir.

Principalele consecinţe obţinute cu ajutorul grupelor I-IV sunt teoria măsurării segmentelor şi a unghiurilor.

Geometria construită cu ajutorul axiomelor grupelor I-IV se numeşte geometrie absolută.

Axioma paralelelor (V)

V. (Axoma paralelelor lui Euclid). Fie o dreaptă oarecare a şi un punct A exterior dreptei a. Atunci în planul determinat de punctul A şi dreapta a, există cel mult o dreaptă care trece prin punctul A şi nu intersectează dreapta a.

Două drepte distincte se numesc paralele dacă ele sunt situate într-un plan şi nu se intersectează.

Este justă următoarea teoremă:

Teoremă. Printr-un punct exterior unei drepte, în planul determinat de punct şi dreaptă, există o paralelă unică la dreapta dată.

Axioma V este echivalentă cu fiecare din următoarele enunţuri:

1) Orice secantă s formează cu dreptele paralele a, b unghiuri alterne interne congruente.

2) Pentru orice triunghi suma unghiurilor este egală cu $180^{\circ}. \!$

3) Există un patrulater în care suma unghiurilor este egală cu $360^{\circ}. \!$

4) Există un dreptunghi.

În baza axiomelor enunţate, poate fi argumentată toată geometria elementară studiată în clasele gimnaziale. Se spune că geometria elementară studiată în clasele anterioare este o interpretare a modelului axiomatic al lui Hilbert de construire a geometriei.

Sursa

• Axiomele geometriei (copie la Wikia